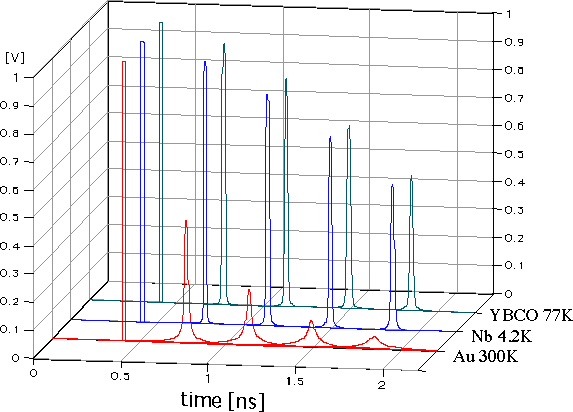
ここで、(3)式のv(0,t)は、0.4[ns]に入力した1[v]のパルス(パルス幅20[ps])であり、(2)式の計算にはFFTを用いた。また減衰定数αについては、(10),(11)式を使った。この時、(10),(11)式の導体損であるが、常伝導体については、文献[1]の値(0.43[dB/cm・GHz1/2])、超伝導体については、Nbで1.63×10-5[dB/cm・GHz2]、YBCOで2.16×10-4[dB/cm・GHz2]の値を用いている。誘電損は共に7.4×10-3[dB/cm・GHz]で、なお計算においてはl=1.55[mm]、G=0.867としている。図では、左から順にL=0,5,10,15,20[cm]の波形を示しており、Lを長くするにつれて、超伝導体では波形を保っているのに対して、常伝導体では波形が減衰しているのが分かる。

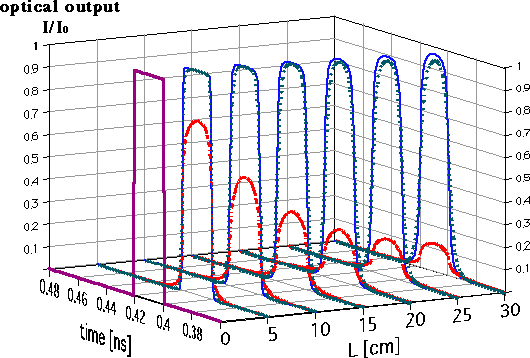
　さらにこの時、(7)式を用いてMZ形光変調器の出力端での光出力強度を図5に示す。ディジタル伝送の場合、パルス波形が用いられるが、図4を見ても分かるように、速度整合が取れていても、電極の損失によりパルス波形が減衰してしまい、その結果、光の変調出力も同様に減衰する。しかし常伝導体の大幅な減衰に対して、超伝導体では波形がわずかしか減衰していないのが図5より分かる。　　

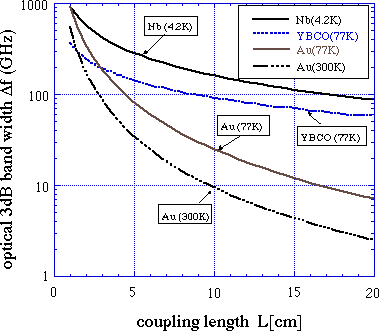
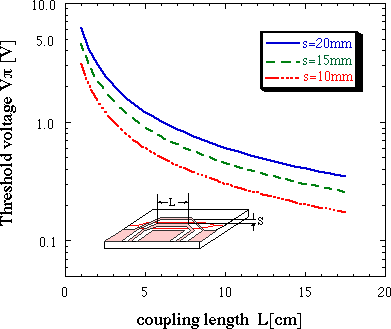
　また、周波数領域において、変調度が周波数に対してどのように変化するのかを調べてみた。速度整合(Nm=N0)の条件下では、変調度は(8)式に従って変化する。図6に電極長に対する3dB帯域幅を示す。この図を見ると、電極長を長くすることにより常伝導体、超伝導体ともに帯域幅が減ってしまう。しかしこの時、(1)式から予想される半波長電圧は図7に示すように、電極長を長くすることによって1[V]以下に減少する。すなわち、超伝導体を用いれば、電極長を長尺化することによって帯域を保ちつつ、駆動電圧の低減化を図れることが分かる。